Fusion Calculus
We developed the fusion calculus, which is a simplification of the pi-calculus with significantly extended expressiveness.
Motivation
The fusion calculus contains the polyadic pi-calculus as a proper subcalculus and thus inherits all its expressive power. The gain is that fusion contains actions akin to updating a shared state, and a scoping construct for bounding their effects. Therefore it is easier to represent computational models such as concurrent constraints formalisms. It is also easy to represent the so called strong reduction strategies in the lambda-calculus, involving reduction under abstraction. In the pi-calculus these tasks require elaborate encodings.
The dramatic main point of this paper is that we achieve these improvements by simplifying the pi-calculus rather than adding features to it. The fusion calculus has only one binding operator where the pi-calculus has two (input and restriction). It has a complete symmetry between input and output actions where the pi-calculus has not. There is only one sensible variety of bisimulation congruence where the pi-calculus has at least three (early, late and open). Proofs about the fusion calculus, for example in complete axiomatizations and full abstraction, therefore are shorter and clearer.
Results
Results for the fusion calculus include
- complete axiomatizations of equivalences
- straight-forward encoding of strong reduction in lambda-calculus, and of rho-calculus (constraint programming)
- pi-calculus as a subcalculus
- symbolic semantics and tool
- coalgebraic models
The Solos Calculus and Solo Diagrams
An interesting sub-calculus of fusion is the solos calculus, where sequentiality is not primitive - actions have no explicit continuations.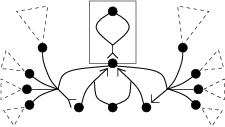 
Without using prefix or summation, we showed that it can express both action prefix and guarded summation. One encoding gives a strong correspondence but uses a match operator; the other yields a slightly weaker correspondence but uses no additional operators. Expressiveness is lost in the solos calculus without match and with actions carrying at most one name; if actions carry at most two names the expressiveness is retained.
We also showed that nested occurrences of replication can be avoided, that the size of replicated terms can be limited to three particles, and that the usual unfolding semantics of replication can be replaced by three simple reduction rules. To illustrate the results and show how the calculus can be efficiently implemented we presented a graphic representation of agents in the solos calculus, adapting ideas from interaction diagrams and pi-nets.
Related work
Independently of our work and of eachother, Yuxi Fu develped the chi-calculus, and Philippa Gardner and Lucian Wischik developed the explicit fusion calculus - both essentially the same as the fusion calculus.
The interchange of names - like an explicit fusion - can be encoded in asynchronous pi-calculus processes called Equators. They were first mentioned by Honda and Yoshida. Merro used equators to encode the asynchronous fusion calculus into the pi-calculus.
See also Lucian Wischik's excellent overview of fusion research
!
Publications
. In Proceedings of CALCO 2005, 2005. (DOI, External link).. In Mathematical Structures in Computer Science, volume 13, number 5, pp 657-683, 2003. (DOI).. In Proceedings of CONCUR'98, volume 1466 of Lecture notes in computer science, pp 99-114, Springer, Berlin, 1998. (DOI).. In Proceedings of ICALP'98, volume 1443 of Lectute notes in computer science, pp 455-469, Springer, Berlin, 1998. (DOI).. In Proceedings of LICS'98, Proceedings / Symposium on Logic in Computer Science, pp 176-185, IEEE Computer Society, Los Alamitos, CA, 1998. (DOI).